This glossary will be broken into two parts: stats that deal with teams, and stats that deal with individuals.
Team Stats
The key high-level team number is efficiency, usually given as “offensive efficiency” or “defensive efficiency” depending on which side of the ball we’re talking. And “net efficiency” is just the difference between the two, making it the overall evaluator of how good a team actually is.
Why use “efficiency” instead of points? Points alone don’t tell us much. For example, is an offense scoring 70 points good or bad? Well, scoring 70 points in 64 possessions is good, but scoring 70 points in 74 possessions is bad. As a result, points per possession is the main building block of basketball advanced stats. To make the numbers prettier, we often multiply PPP by 100 to get efficiency: a team scoring 1.247 points per possession has an offensive efficiency of 124.7, meaning that they scored 124.7 points per 100 possessions. This can be done for the defense as well.
Using efficiency instead of points is a form of standardization. Standardizing is better than using raw numbers. You’ll need most numbers set to “per 40 minutes” (standardized, but not pace adjusted), and “per 100 possessions” (standardized and pace adjusted). That way we can compare different teams and players directly.
Adjusting for Opponent
All of the team-level numbers that we post are adjusted for opponent. Is a team’s 101.7 offensive efficiency in a game good? Well, if they were playing Houston, yes, but if they were playing Mississippi Valley State, then no.
To calculate opponent-adjusted offensive efficiency for a single team for an entire season, we use the following calculation:
(Team Off. Efficiency x D-1 Average Off. Efficiency) / Average Def. Efficiency of All Opponents
This tells us how much better than their opponents’ average a team was all season. All of the stats we use can be adjusted in this way.
Shot Creation versus Shot Making
Next to efficiency, the next two important stats measure two distinct parts of a basketball game: shot creation and shot making.
Think of it this way: how many points is a rebound worth? None. But rebounds are still important because they create a chance to score. So they fall under the “shot creation” group of stats.
The stat that measures shot creation is called effective possession ratio, or EPR. It’s how many shots a team creates out of 100 possessions. So if a team has an EPR of 96.7, that means that for every 100 possessions, they’ll get 96.7 shot chances. Offensive rebounds make EPR go up, and turnovers make it go down. The formula is really simple:
EPR = 100 * (Possessions + Offensive Rebounds – Turnovers) / Possessions
A team’s ability to turn shot chances into points is measured by true shooting, or TS%. True shooting measures points per shot chance, treated all shots as 2-point field goal attempts. So a made 3-pointer actually counts as 1.5 makes, since it’s worth 1.5X as many points as a 2-point field goal. Here’s the true shooting formula:
TS% = 0.5 * Points / (Field Goal Attempts + 0.44 * Free Throw Attempts)
The “0.44” on free throw attempts is because on average, about 44% of free throws actually end a possession. You’d think it would be 50% (two-shot foul, second shot ends the possession), but there are lots of other free throw situations: and-ones, missed front end of one-and-one, three-shot fouls. It averages out to about 44% of free throws actually ending a possession.
Now let’s make it really simple:
Offensive Efficiency = EPR * 2 * TS%
True shooting is multiplied by two because we standardized it to 2-point shots. The two components of offensive efficiency can simply be multiplied to together to create it. Easy, right?
Other Stats
Here’s a list of other stats we use.
- Scoring %. Percent of team possessions where the offense scores (doesn’t matter how many points).
- Transition %. Percent of team possessions that include a shot taken within 10 seconds of receiving the ball. Note that this isn’t the same thing as “fast break”… fast breaks require that all 10 players not be down the floor together, but transition includes no such requirement.
- Average Possession Length (APL). Average length of possessions, in seconds.
- Offensive Rebound %. Percent of team’s missed shots where they get the offensive rebound.
- Turnover %. Percent of team possessions that end in a turnover.
- Free Throws Attempted per Field Goal Attempted. Number of free throws attempted per field goal attempted.
- Effective Field Goal % (eFG%). Field goal percent, but with made 3-pointers counting as 1.5 makes, reflecting their higher points value. This helps account for the fact that shot all shots are worth the same: a 40% shooter is good if he shoots 3s but bad if he shoots 2s. eFG% would make that 40% 3-point shooter into a 60% eFG% shooter.
- Midrange. All 2-point shots that are not recorded as dunks, layups, or tip-ins. We classify all field goal attempts into three buckets: 3-pointers, midrange, and rim.
- 3-point usage / midrange usage / rim usage. Percent of a team’s field goal attempts that come from those three levels.
Example
Here’s an example we use in our recap articles. This is from the Arkansas-Michigan game in 2024.
First, the possession breakdown:
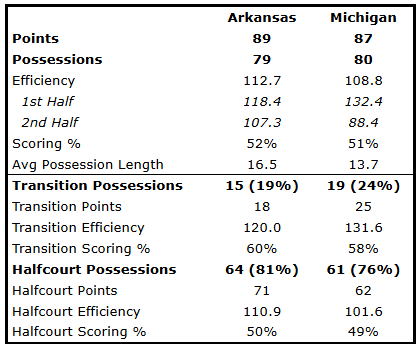
We see the overall numbers (offensive efficiency, scoring %), how fast each team played, and how each team did in transition versus halfcourt.
Now, the other stats:
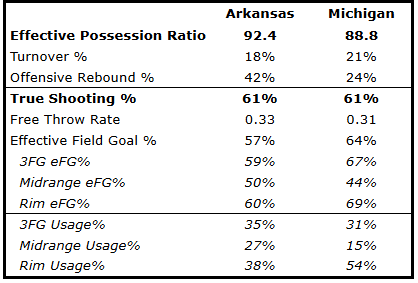
The two teams had identical true shooting numbers, but the Hogs won by winning the battle on the boards. They grabbed 42% of their missed field goals, compared to just 24% for Michigan.
Individual Stats
Our individual stats have gone through several changes, but the current form is likely what will remain for a while, as it is roughly in line with the standard for basketball analytics.
Check out this handy chart, giving an overview of the different types of advanced individual stats and how useful they are:
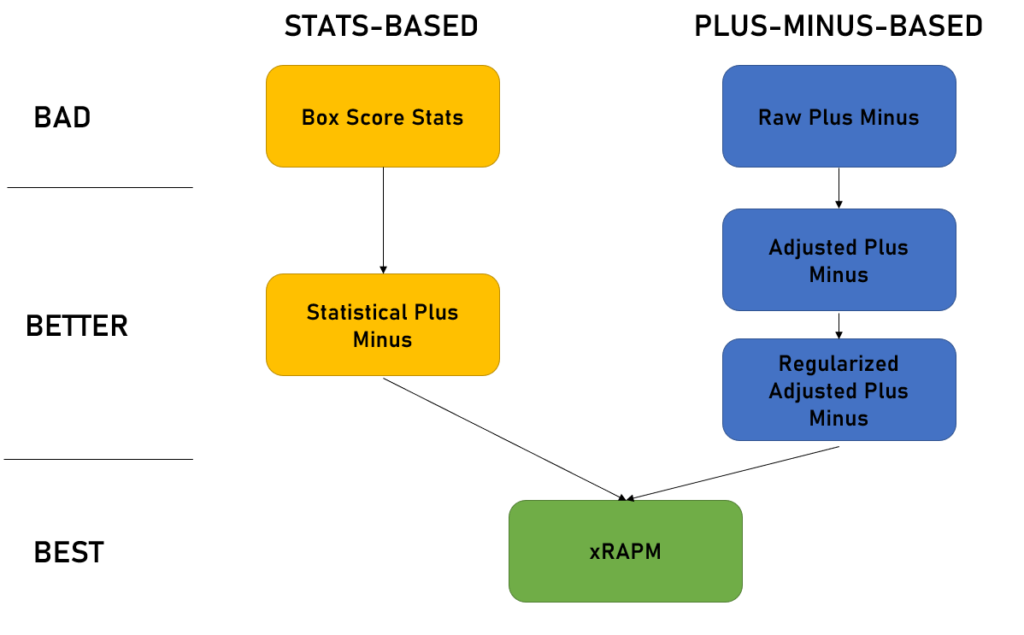
To understand what those fancy ones at the bottom are, let’s walk through each of these six stats one by one.
Stat-Based Numbers
One way to evaluate players is just by looking at their raw box score stats. Is that a good way to go? Obviously not. A player’s raw points per game don’t really tell you all that much about how good he is. You can do slightly better by setting his stats to per 40 minutes or per 100 possessions, but you’re still limited to what’s in the box score, and there are a lot of stats there.
Consider two players:
- Player 1: 12 points per 40 minutes on 55% eFG%
- Player 2: 14 points per 40 minutes on 35% eFG%
Who is probably helping his team more? I would say the first one, since he’s so much more efficient. Do you agree?
But in order to decide that the first player was better, we had to introduce a second stat (eFG%). But there a ton of stats out there. What if Player 2 is an amazing rebounder who also gets a lot of steals? That changes it again. Continuing to introduce numbers makes it more and more complicated.
One solution is to distill all the box score stats into a single number that tries to estimate how much better a player makes his team, using only box stats. This is statistical plus minus. It’s a pretty big improvement over just looking at basic stats, though it still has some shortcomings.
The most popular stat within this group is Box Plus Minus, or BPM. It sticks a coefficient onto all of a player’s box score stats, weighting them based on how important they are to a team’s success. The formula is a bit complicated, but the output is an estimate of how much a player contributes to his team overall. So a player with a +8 BPM is making his team 8 points better per 100 possessions. BPM has both offensive (OBPM) and defensive components (DBPM), which isolate stats impacting offense and defense.
So is this number actually accurate? Well, sort of. If you look at a list of top NBA players by BPM, it passes a gut check. Players we normally think are good have high BPMs, and there’s always a few surprises that can be rationalized. But statistical plus minus has a serious problem: it is limited to box score stats. That hurts it a bit on offense – things like spacing, off-ball movement, screening, good passes that don’t lead to an assist won’t show up in the box score – but it really hurts it on defense. DBPM is widely considered to be totally unreliable. It is using only steals, blocks, and defensive rebounds, and playing defense is about so much more than those things.
In order to get a truly accurate stat, we have to move beyond box score numbers.
Plus Minus Numbers
Plus-minus is a simple enough concept: if Arkansas outscores an opponent 60-56 with Player A on the court, then his plus-minus is +4. No box score stats are needed.
For a single game, plus minus is pretty harmless. It doesn’t tell us much, but stark contrasts can sometimes be made. But raw plus minus has a major issue: collinearity. That’s a math term that refers to a case where multiple variables may be influencing the same result, and it’s impossible to isolate the impact of each variable.
Raw plus minus will reward bad players on good teams, because those players are on the floor for good moments, even if they aren’t doing anything to cause them. A few years ago, Gonzaga had the top 3 players in the country in raw plus minus per 40 minutes. Did the Zags really have the best three players in the nation? Obviously not. They just beat the tar out of a bunch of teams and those three were on the floor for a lot of it.
To improve raw plus minus and deal with collinearity, we can run a regression over every possession in a season. A regression, instead of adding up all the plus minus numbers, will focus on more broad patterns: how often does the team get better when a certain player comes into the game? The result, called adjusted plus minus, is widely considered to be much better than raw plus minus.
But adjusted plus minus has a major issue: it often exaggerates small differences. If two players play every single moment together for an entire season, and then one player checks out of the game in the last minute of the year, and a walk-on hits a 3 while he’s on the bench, the second player (who was still in the game) will get a monster boost to his APM, because the regression model will see what happened and assume that the first player was holding back the second one all along. That’s a silly example, but that’s what can happen.
In order to correct for this, we introduce to our regression a regularization factor. Our regression is now what’s called an L2 (Tikhonov) regression. This means that the model starts with an assumption that all players are worth zero, and requires significant evidence to deviate from that assumption. This helps curb the wild swings. The output is now called regularized adjusted plus minus, or RAPM.
RAPM is the gold standard of advanced individual stats. It was actually invented for hockey but has been applied to basketball in the same way. It tells us how much better a player makes his team, regardless of who he shares the floor with. It’s the perfect stat, right?
Unfortunately, no. It has a major flaw. Because the model is biased toward zero, the amount of data required to make it stable and accurate is enormous. In the NBA, RAPM is usually given over multiple years and single-year RAPM is generally considered unstable and only somewhat useful. That creates three problems for us:
- College seasons are even shorter than NBA seasons, so single-year RAPM is even more unstable
- Multi-year RAPM is harder for college players, who generally have only a few years of eligibility
- We want to know how good a player is this year, and including data from several years ago – though necessary to make the model accurate – doesn’t tell us how good a player is now
We used single-year RAPM throughout the 2023 season, but we saw major shifts in individuals’ RAPMs over the season. Did those players get better or worse, or was RAPM just in flux? There’s no way to be sure.
xRAPM / FV Score
There is one way to fix RAPM for use in single seasons. Think about it real quick: the issue with RAPM is that it starts by assuming all players are equal (at zero), and then demands an enormous amount of data to move away from that assumption for each player. How do we fix that?
Well, there’s one thing we do know: not all players are equal. What if we could tell the model that? Turns out, we can! In data science, this is called a prior: something that is known about the data that the model can use as a starting point.
What kind of prior could we create for the model? What do we have at our disposal that could help us make assumptions about which players are better? Imagine a sequence: Arkansas gets the ball, and Player A makes a shot. Then Player B gets a steal on the other end. For that set of one offensive and one defensive possession, Arkansas was +2. How do we know who was responsible for Arkansas going +2? Well, we know that Player A needs at least some credit, since he made the shot, and Player B needs at least some credit, since he got a steal.
Turns out, we can use box score stats as priors. We use a raw version of BPM to feed the model as an assumption. We know it’s not perfectly accurate, but it doesn’t have to be. It just needs to give the model a starting assumption. The model then runs its regression. Instead of needing mountains of evidence to move away from zero, it now needs mountains of evidence to move away from the prior. His box score stats are now baked in, so if a player routinely makes his team better with non-box contributions, the output will move higher than the prior. If he routinely makes his team worse with his non-box contributions, the output will move lower than the prior.
This output, called expected RAPM or xRAPM, is basically just a combination of BPM and RAPM, and can be thought of as a more accurate version of each. For our use – a single college season – it is much closer to BPM than RAPM. For a full NBA season, it ends up trending closer to RAPM than BPM, because the larger sample size of games allows the model to continue to drift towards its actual findings rather than sticking to the prior.
How accurate is xRAPM? It’s the best we have. It’s quite predictive from season-to-season, even for players that transfer. Is it perfect? No. It is important to note that there is no “perfect stat”. Here at Fayette Villains, we will never tell you to only look at our numbers over watching film, considering the role of scheme and coaching, and other factors. But at its core, basketball is a numbers game: if I have 70 points and you have 60, then I win, regardless of how pretty your film looks. So the desire to figure out the cause of “scoring more points” is an exercise in mathematics.
Anyway, all of the cutting-edge stats you see out there in the NBA are xRAPM models: ESPN’s RPM, 538’s RAPTOR, BBall Index’s LEBRON. All of those are just xRAPM. They calculate their priors slightly differently and have slightly different methods of doing the regression, but they are all essentially the same thing. Here at Fayette Villains, we like to normalize all the xRAPM outputs from a single season so they sit on a scale of 0-100, which we call FV Score. It’s just a grade, so an OFV Score of 93 means that player’s xORAPM output was in the 93rd percentile of all Division I players.
For a high-major team like Arkansas with major NCAA Tournament aspirations, grades of 98+ are all-SEC or even all-American levels, grades of 90+ are quality starters, grades in the 80s are high-usage role players or lower-end starters, and grades in the 70s are down-in-the-rotation role players. Players with grades below 70 probably aren’t helping their team much. Those expectations differ by quality of team, but that’s for a team like Arkansas most years.
In the Eric Musselman era, Jaylin Williams in 2022 had the highest xRAPM. The top five overall, plus offense and defense, were posted to Twitter:
For reference, here are the top players in WAR in the 2023 season (Anthony Black, who led the Hogs, finished 26th):
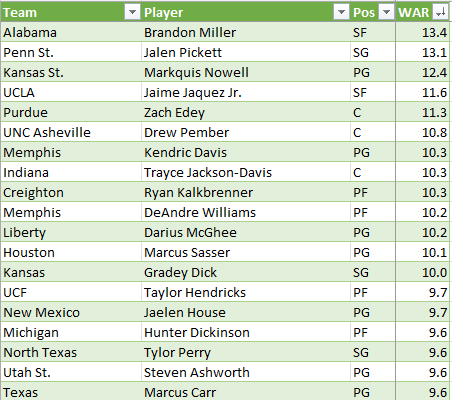
Other Stats
- Usage %. This is the percentage of a team’s shots and turnovers that one player is responsible for while he’s on the floor. Since there are five players on the floor for the offense, 20% is “moderate” usage. Above about 22% is considered “high usage”, while below about 18% is considered “low usage”.
- Team Efficiency. This the player’s on-floor team offensive and defensive efficiencies. It simply answers the question of how good the team is while that player is out there.
- Rating. A player’s offensive and defensive rating is different from his team efficiency. It starts with team efficiency and then adds in box score stats, so in many ways, it’s trying to do the same thing as xRAPM, though it’s less accurate. Still interesting to look at.
- Box Creation. This clever stat estimates how much pressure a player puts on the defense. The inputs to calculate are points, turnovers, assists, 3-point attempts, and 3-point %, as research has shown that these stats help pressure the defense the most. 3-point shooting spaces the defense, assists create points that other players score, and points and turnovers are indicative of volume. Generally, you want to have at least one player with high Box Creation on the floor at all times or your offense will struggle, and high Box Creation players can set their low-usage teammates up for shots, so it often correlates with high plus minus numbers, at least on offense.
- Kills. A “kill” is a steal, block, or drawn charge. Kills are forceful ends to possessions. Players that get a lot of kills are major defensive playmakers. We report kills per 40 minutes and kills per personal foul, as trying to get kills carries a risk of a foul. Players with good kill-per-foul numbers are generally able to hold their own while defending more athletic opponents.
